The Sloan Digital Sky Survey has recently finished mapping more of the universe than ever before. To create the map the Survey zeroed in on quasars, supermassive black holes at the center of galaxies and bright enough to be seen across expansive distances. But, because they are so far away, our concept of distance must be carefully described.
For stars visible in our night sky, distance is defined as the physical distance between the star and our sun. The measurement used for this is called a parsec. A parsec is determined by calculating a star’s parallax shift in arcseconds. The very word parsec is an abbreviation of these two words, parallax, and arcsecond. For example, Sirius is 2.6 parsecs away, meaning its parallax shift is 2.6 arcseconds. Therefore its parallax shift, or how much its position changes in the night sky as the Earth orbits the sun, is one arcsecond, or 1/3600 degree of an arc across the sky. The closer the star, the smaller it’s parallax shift.
While an astronomer may use a parsec to measure the distance of a star, most of us are more familiar with a light year measurement. The time it takes a stars’ light to be visible from Earth. Using Sirius as an example again, it’s light takes 8.6 years to reach or, or 8.6 light years. But if we wanted to travel to this bright star, we would need to adjust our trajectory to account for it’s ever changing location as the universe would expand during the eight and half years long journey, if we could travel at the speed of light. However, the difference would not be that different given that it’s fairly close to Earth.
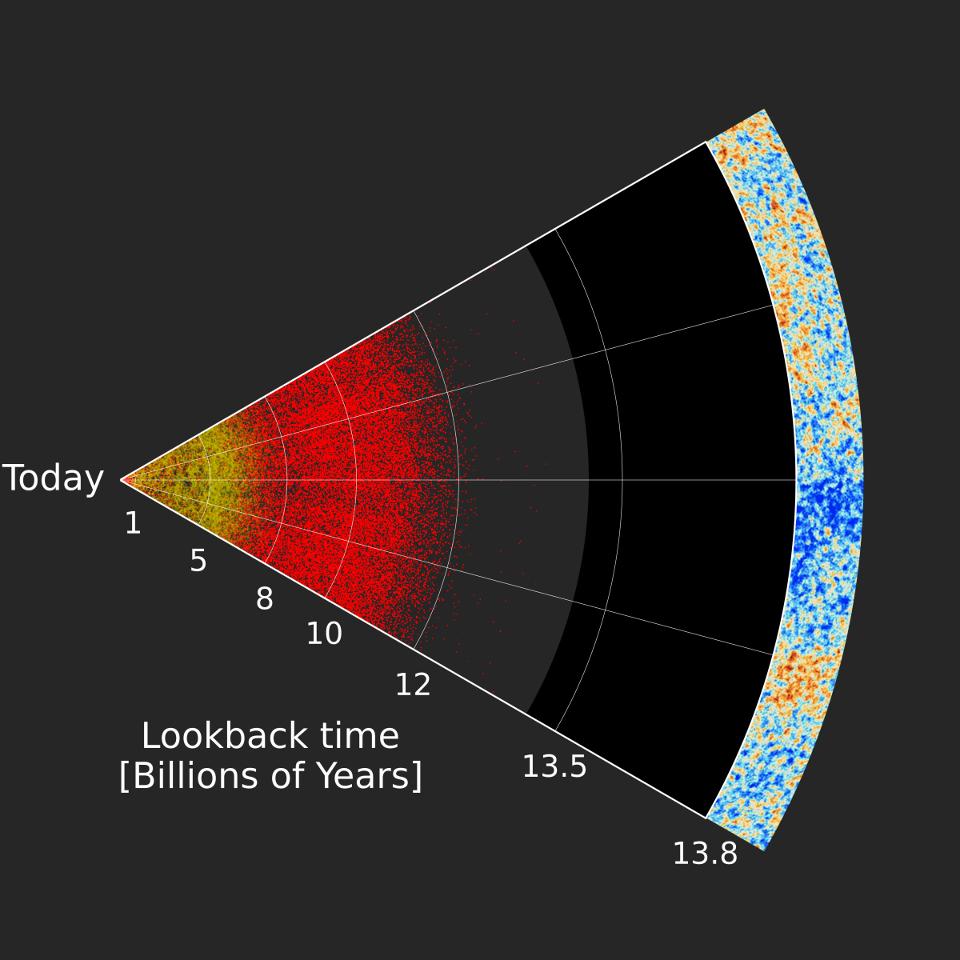
Because a star’s parallax shift can be so small, it is only a useful for the way to measure objects about 10,000 light years away. Beyond that, the parallax shift becomes too small to measure accurately. Further objects must be measured by different means, though it can still be expressed in parsecs and lightyears. Another often used method is based on a type of star called a Cepheid variable. These variable stars have a specific ratio between their general brightness and how rapidly they fluctuate between dark and bright. Observing them over time allows us to track their variability and calculate a star’s distance. The fluctuations of the Cepheid variables in the Andromeda galaxy indicate it is 2.5 million light years away or 766,000 parsecs. But, like with stars, galaxies move. During a 2.5 million year journey from Earth to the Andromeda galaxy, it will have moved 1,500 light years from our original measurement of its location. Compared to 2.5 million, 1,500 light years is only a small fraction, but it is not an insignificant distance.
For the furthermost away galaxies, distance is even harder to gauge. By measuring the movement of other galaxies, using their light’s redshift, we know that the further away galaxies are the a greater their redshift is, because of the expansion of the universe. Due to dark energy, the distance between objects in the cosmos is constantly increasing, making it difficult to define galactic distance.
The easiest gauge we can use is the measurement of a distant galaxy’s redshift, often expressed as z. Z represents a fractional value of a particular wavelength change between it’s shifted and unshifted state. The top limit of this range is 12, so far as we’ve observed, so let’s use an example of half that: a galaxy where z=6. How far away is a redshift z=6 galaxy?
Redshift is caused by two factors: the movement of space itself, known as cosmological redshift, and the movement of a galaxy through space, usually called Doppler redshift. Although we cannot tell the difference between them through observation, we know from tracking a variety of other galaxies that the Doppler redshift is small enough to be insignificant in calculations. Therefore we can safely assume that universal expansion causes most galaxy redshift. To use this information to calculate the distance of our z=6 quasar, we have to consider how, over time, the universe is expanding, which depends on our cosmological model. The most commonly used model is the concordance, or ΛCDM, model, dark matter and dark energy dominated the universe. Again, assuming it is an accurate model, which it pretty much is, we can calculate distances. But first, we must carefully clarify what we mean by distances.
Using our previous definition of a parsec, using the light we can see, how far is a galaxy with a redshift of z=6? A more accurate way to phrase the question is “When light left this galaxy, how far away was it?” It turns out a redshift z=6 quasar is approximately 1.2 billion parsecs. It’s appealing to transform this measurement to light years, simply saying it’s 3.9 billion light-years away, but that would be inaccurate. Taking into consideration cosmological expansion, the travel time of the light was 12.8 billion years. Therefore the 1.2 billion parsecs took 12.8 billion years for the light to travel to Earth. As this is a common understanding of the age of light, we might say that we are seeing into the past, seeing our redshift z=6 galaxy as it was 12.8 billion years ago.
On the other hand, that can make the discussion that much more confusing. The travel time of the light may be 12.8 billion years, but the galaxy was only 3.9 billion light years away when the light started its journey. The quasar the light left moved away from us as space expanded (the cosmological redshift), while the light moved toward us as the universe expanded (Doppler redshift). This simultaneous motion accounts for 8.4 billion parsecs or 27 billion light years.
Every one of these distinct ways to describe distance is valid in its own right while being very different from one another. This explains why most astronomers try to use a single type of definition, that is redshift when discussing distance.
More News to Read
- Presenting The ‘Chit’ — The One and Only Chemical Hard Drive
- Abnormal Proteins Apparent in Alzheimer’s, Parkinson’s, and Huntingdon’s Patients
- What’s the Deal With Transformative Artificial Intelligence?
- Space Station Experiments Could Prove that Dark Matter Destroys Itself
- A New Method Tracks Unique Neurons and Brain Activity to Specific Actions in Zebrafish











